拜占庭将军问题

发表于
分布式系统经典共识算法拜占庭将军问题，附国科大薛键老师云计算课后作业的拜占庭将军问题例题。

介绍

拜占庭将军问题是分布式系统中为达成一致性和容错性的解决算法。

理论基础

分布式计算的理论基础是由基本概念，架构模式，关键技术构成。
基本概念：分布式计算是独立计算机集合
架构模式：软件：数据中心流 系统：客户端/服务器对等
关键技术：面向过程：IPC->RPC 面向对象：分布式对象框架 面向服务：SOA->Web服务->面向服务计算->云计算
由上述理论基础，构成分布式计算，但不足以解决实现层面的问题，比如可用性(availability)，一致性(consistency)等。
但是要达到实现层面是有牺牲的，正如不存在第一类永动机，由此提出分布式系统的CAP理论，一个分布式系统最多只能同时满足一致性(consistency),可用性(availability)，分区容错性(partition tolerance)三项中的两项。
拜占庭将军问题即为了达到一致性和分区容错性(叛徒存在？)牺牲了部分可用性，在一定时间后能达成一致。

拜占庭将军问题

拜占庭将军问题是问了解决分布式系统中的一致性问题，即多个节点对外呈现一致数据的状态，这种状态需要通过某种共识算法来达成，拜占庭将军问题正是这种算法，通过将节点比喻成将军，描述了分布式系统中多个节点对某个状态达成一致结果的过程。虽然拜占庭将军问题对故障的假设较为一般，但是同时假设节点之间通信不会出现错误，不存在信道问题，在现实中不常见。另一个缺点是算法复杂度过高。
举个🌰，如果某个节点想要修改一个数据，需要其它节点共同来决定能不能改，避免出现如果节点被异常程序攻击，恶意修改数据的情况。对应拜占庭将军就是通过投票来决定是否要进攻，下面是问题描述:

1
2
3
4
5
6
拜占庭帝国派出多支军队共同围困一座城市，每一支军队由一个将军率领。
为了简化问题，将各支军队的行动策略限定为进攻或撤退两种。如果大家行动不一致可能会造成灾难性后果，
因此各位将军必须通过投票来达成一致，即所有军队一起进攻或一起撤退。
因为各位将军分处城市不同方向，他们只能通过信使互相联系。
在投票过程中每位将军都将自己的决定通过信使分别通知其他所有将军，
这样一来每位将军根据自己的决定和其他将军送来的信息就可以知道共同的投票结果而决定行动策略。

拜占庭故障：将军中出现叛徒，发送干扰投票信息。这种故障比分布式系统中的故障还要严重，分布式系统中的故障仅仅是无限期延迟，并不会刻意干扰投票。
拜占庭容错：如果存在叛徒情况下，忠诚将军仍能就战略问题达成一致并反应真实意图，称为达到了拜占庭容错。
方案1:将军𝑖将其消息𝑣 𝑖 直接发送给其他每个将军，所有将军按照少数服从多数的原则行事。
方案1是存在问题的，如果将军中存在叛徒，干扰投票，忠诚将军服从的可能不是同一个命令
怎么解决方案1呢，将军i将消息传递给将军j,将军j再问问其它将军收到的将军i的消息是什么，然后在这些消息里取一个majority作为将军i的真正消息，具体可以看后面的例子。
这里描述的都是基于口头消息传递的拜占庭将军的问题，如果是基于签名传递的问题，不存在这种问题，因为叛徒无法伪造签名。基于口头消息传递的拜占庭将军问题可解的条件：

1
2
3
一个主将必须将一个命令传达给他的𝑛 − 1个副将，使得:
IC1. 所有忠诚的副将服从相同的命令;
IC2. 如果主将是忠诚的，则每个忠诚的副将服从他发出的命令。

在这种情况下，如果少于3m+1个将军搞不定m个叛徒，具体解释可以看论文里的图：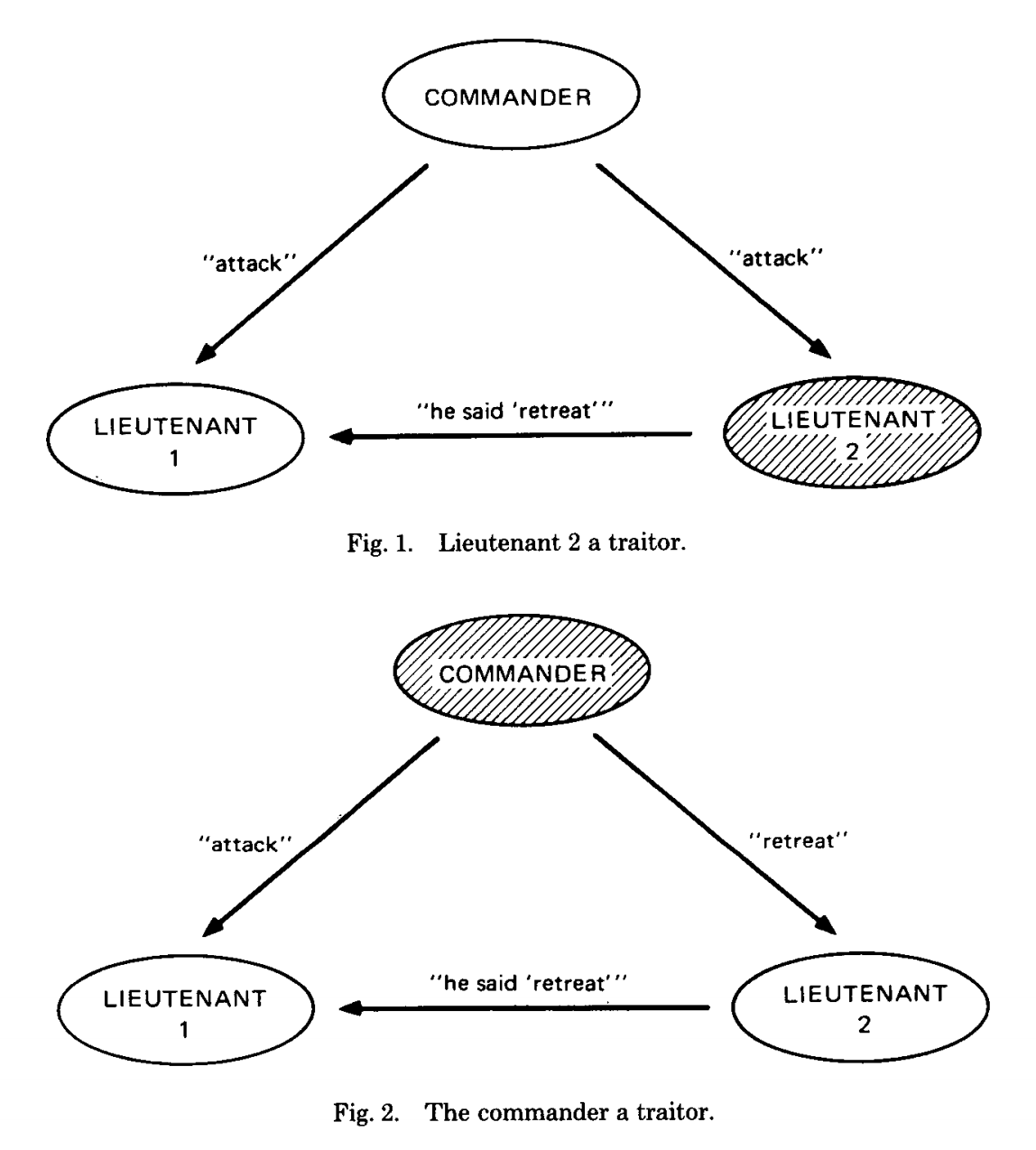
image1
主将是叛徒无法满足ic2,将军是叛徒无法满足ic1，不管是主将是叛徒还是将军是叛徒，忠诚将军都会confuse。
解决口头消息的算法：

1
2
3
4
5
6
7
算法 𝐎𝐌 𝒎 , 𝒎 > 𝟎

1 主将将消息发送给每个副将
2 发送消息：对每一个副将𝑖:记𝑣𝑖 为其从主将获得的消息或者“撤退”(如果没有收到消息)，
副将𝑖作为主将调用算法 𝐎𝐌(𝒎 − 𝟏)，将消息𝑣𝑖发送给另外𝑛 − 2个副将
3 回收消息：对每一个副将𝑖:记𝑣j 𝑗 ≠ 𝑖 为其在第2步中从副将𝑗处获得的消息或者“撤退”(如果没有收到该消息)，
副将𝑖采纳𝐦𝐚𝐣𝐨𝐫𝐢𝐭𝐲 𝑣1,⋯,𝑣𝑛−1

m代表消息传几轮，如果m是0，则主将发一次消息，副将直接采用主将发送的消息。是一个分布式递归算法。分布式体现在是不同将军去执行的，递归体现在majority里的v1…也是majority投票的大多数。由算法公式可知，拜占庭将军问题复杂度达到O(n!)，效率非常低。

拜占庭将军例子

国科大薛键老师云计算课程的作业，结合例子体会拜占庭将军问题对算法的理解会更清晰。
问题：
假定现在有7个将军：主将和副将1~6，其中主将和副将6是叛徒，在这种情况下试推导基于口头消息的共识算法的执行过程，并说明忠诚的将军如何就“进攻”还是“撤退”达成共识。
解：
因为主将是叛徒，不需要满足ic2，只需满足ic1所有忠诚副将(1-5)服从相同命令
一般性讨论，假设每个将军发送的消息是X,X(0-1)代表消息从0发给1，X(0-1-2)代表1将0发给它的消息转发给2，0给1的消息发给2.
1.主将第一轮发送消息(OM2)：X(0-1), X(0-2),X(0-3),X(0-4),X(0-5)
2.第二轮(OM1):
副将1:X(0-1-2)，X(0-1-3)，X(0-1-4)，X(0-1-5)，X(0-1-6)
副将2:X(0-2-1), X(0-2-3),X(0-2-4), X(0-2-5), X(0-2-6)
副将3:X(0-3-1)，X(0-3-2)，X(0-3-4)，X(0-3-5)，X(0-3-6)
副将4:X(0-4-1),X(0-4-2),X(0-4-3),X(0-4-5),X(0-4-6)
副将5:X(0-5-1),X(0-5-2),X(0-5-3),X(0-5-4),X(0-5-6)
3.第三轮(OM0)
这一轮每个副将将刚从其它将军手里接过来的主将消息发给其它将军，以1将军为例，1把从2将军获得的0-2消息转给3，4，5，6将军，从3将军获得的0-3消息转给2,4,5,6将军，依次类推，每个副将一共需要发送5x4=20条消息，这里仅列出副将1需要发消息的情况。
副将1:
转发从副将2来的消息X(0-2-1): X(0-2-1-3),X(0-2-1-4),X(0-2-1-5),X(0-2-1-6)
转发从副将3来的消息X(0-3-1)：X(0-3-1-2),X(0-3-1-4),X(0-3-1-5),X(0-3-1-6)
转发从副将4来的消息X(0-4-1): X(0-4-1-2),X(0-4-1-3),X(0-4-1-5),X(0-4-1-6)
转发从副将5来的消息X(0-5-1): X(0-5-1-2),X(0-5-1-3),X(0-5-1-4),X(0-5-1-6)
转发从副将6来的消息X(0-6-1): X(0-6-1-2),X(0-6-1-3),X(0-6-1-4),X(0-6-1-5)
…
投票：
这里也做个一般性的推导：
在j将军手中来自i将军的消息
X(i-j)=majority(X(0-i-j),X(0-i-p-j)),p=1,2,3,4,5,6 p≠i,j, i≠0,j≠0
因为主将不忠诚，剩下的i,j,p中只有可能出现1个不忠诚将军。p是除了i,j将军其它将军的集合。
1) 假设i不忠诚：
则出现在p中的将军和j将军都忠诚，将严格传达收到的命令
则X(0-i-j)=X(0-i), i将军可能会故意转发错误信息，X(0-i-p-j)=X(0-i-p)
此时X(i-j)=majority(X(0-i-j),X(0-i-p)),p=1,2,3,4,5,6 p≠i,j，p和j是将军集合中除了不忠诚将军以外的所有将军。
对于这个题而言，i=6
副将1:X(6-1)=majority(X(0-6-1),X(0-6-2)，X(0-6-3),X(0-6-4),X(0-6-5))
副将2:X(6-2)=majority(X(0-6-2),X(0-6-1)，X(0-6-3),X(0-6-4),X(0-6-5))
副将3:X(6-3)=majority(X(0-6-3),X(0-6-1)，X(0-6-2),X(0-6-4),X(0-6-5))
副将4:X(6-4)=majority(X(0-6-4),X(0-6-1)，X(0-6-2),X(0-6-3),X(0-6-5))
副将5:X(6-5)=majority(X(0-6-5),X(0-6-1)，X(0-6-2),X(0-6-3),X(0-6-4))
可以看出X(6-n)=majority(X(0-6-1),X(0-6-2)，X(0-6-3),X(0-6-4),X(0-6-5))是相等的。
2)假设j不忠诚:
则p中将军和i将军都忠诚，由于j只是个接收者，此时有X(0-i-p-j)=X(0-i-j)=X(0-i)
此时X(i-j)=majority(X(0-i-j),X(0-i-p-j))=X(0-i)
其实这种情况也可以不用讨论，因为X(i-j)是j将军用来最后投票的，j不忠诚，所以它最后的决策我们并不关心。
3)假设p中存在不忠诚将领:
i,j都忠诚，则X(0-i-j)=X(0-i)
在p集合中，有4位将军，有一位不忠诚，对于其它三位有:X(0-i-p-j)=X(0-i)
对于不忠诚将军，假设为p1有X(0-i-p-j)=X(0-i-p1-j)
最终投票环节X(i-j)=majority(X(0-i),X(0-i)，X(0-i)，X(0-i)，X(0-i-p1-j))=X(0-i)
以副将1投票为例：将所有发给副将1的消息投票，其中忠诚将军的投票可以化简majority(X(0-1),X(2-1),X(3-1),X(4-1),X(5-1),X(6-1)),其中X(2-1)是个递归调用，从3，4，5，6转发过来的2发给它们的消息中取一个majority，X(2-1)=majority(X(0-2-1),X(0-2-3-1),X(0-2-4-1),X(0-2-5-1),X(0-2-6-1)),而因为1,2,3,4,5都是忠诚将领，X(0-2-1)=X(0-2-3-1)=X(0-2-4-1)=X(0-2-5-1)=X(0-2),X(2-1)=X(0-2)，同理，X(3-1)=X(0-3),对叛徒副将6，X(6-1)=majority(X(0-6-1),X(0-6-2-1),X(0-6-3-1),X(0-6-4-1),X(0-6-5-1))=majority(X(0-6-1),X(0-6-2),X(0-6-3),X(0-6-4),X(0-6-5))
则X1 = majority(X(0-1),X(0-2),X(0-3),X(0-4),X(0-5),X(6-1))，由上面的推导可得Xn=majority(X(0-1),X(0-2),X(0-3),X(0-4),X(0-5),X(6-n))
由第一种情况的推导知X(6-n)对每一位忠诚将军都相同。
因此无论叛徒主将怎么安排发给6位将军的信息，忠诚副将都会达成一致。